Simplicity itself

As familiar as was his account of complex entities, as familiar is also Wolff's description of simple entities, which in many cases simply have characteristics opposite to characteristics of complex substances. Previously I characterised Wolffian simple things as units of forces, which is quite correct still in light of Latin ontology, but one must not assume that complex entities could not then be described in terms of forces. Instead, the notion of force is something common to both simple and complex entities.

To understand what Wolff means by a force, one must begin with the notion of modes that we know to be characteristics that can be changed without changing the essential identity of a thing. Now, consistent collections of modes define a certain state. Such states, if they happen to be instantiated, belong to some thing, which can then be called the subject of these states, which are then adjunct to the subject. Note that the notion of subject, just like the notion of essence, is context dependent: in geometry we might take certain figure as stable, while in physics this figure could also be mutable.

In some cases, the change of states can be explained through the subject of change – then the change can be called an action of the subject, while in the opposite case it could be called passion. Thus, while if I voluntarily jump from a plane, the subsequent fall is my action, if on the other hand I am thrown from a plane, the fall is my passion. A subject undergoing an action can be called an agent, while a subject undergoing a passion can be called patient.

Furthermore, corresponding to action and passion, a thing has corresponding possibilities for action and passion or active potentiality and passive potentiality, the former of which Wolff also calls faculty. Without these potentialities actions and passions could not occur, but as mere possibilities they still require something in order to be activated.

In case of actions, this activating element is finally called force. What a force is or how it will be generated should not yet be apparent from this nominal definition. Still, it is quite clear from the definition that it makes no sense to speak of a force if there is no action that it activates, unless there is some opposing force resisting this activation.

This is as far as conceptual analysis takes us. From empirical considerations Wolff concludes that we could describe force as consisting of conatus. Conatus is a peculiar notion, common to many early modern thinkers, such as Spinoza, meaning a sort of life force of a thing that aimed at preventing the destruction of the thing. In physical contexts, conatus was often identified with impetus, the habit of bodies to remain in the same state of movement – this tendency was thought to be due to some internal yearning of bodies.

One obvious aim of this talk of conatus or impetus is to introduce the possibility to quantify forces – forces can be connected to the actions they trigger, and we can thus present forces as vectors. Because of their quantitative nature, forces can be combined (basic principle for this possibility is easily seen in a so-called parallelogram of force). Thus, we can regard forces of composite entities as combinations of forces of simple entities.

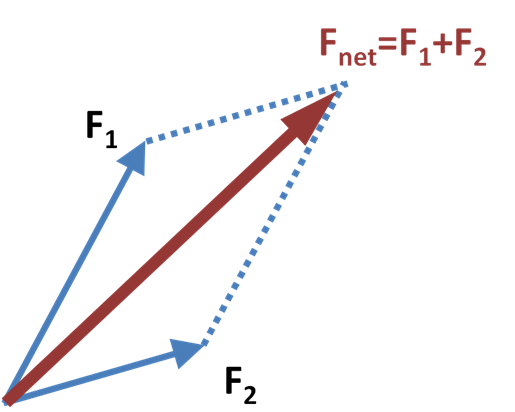Parallelogram of forces: when forces F1 and F2 are the only forces affecting a thing the resulting movement is described by their sum

The mathematics of forces is one step in Wolff's project of quantifying philosophy. A final step is taken with the notion of grade, which Wolff defines as a characteristic of qualities that can be used to distinguish different (spatial or temporal) instances of same quality (thus, two apples might have a different tinge of green). Now, Wolff notes that it is possible to create at least a fictitious quantification for the grades (just think of a temperature scale – if a temperature of air rises two grades, this does not happen because of adding two individual grades of warmth to air). Because qualities were originally the only impediment of the quantification program, Wolff thinks he has solved the problem suggested by his critics.

The final piece in separating complex and simple entities is the notion of substance. Here Wolff begins by distinguishing between what is mutable (that which can be changed without it losing its essential identity) and what is only perdurable (that which can exist for a time without losing its essential identity). Now, Wolff's interest lies in perdurable things: cows, shadows, colours, you name it. Some of these perdurable entities are not mutable, some of them are. According to Wolff, this distinction among perdurables captures the traditional distinction between accidences and substances. This might need some explanation. Consider a traditional example of an accidence, such as certain shade of colour. It can definitely exist for a while, say, on some surface, but when you try to change it, it will change into a different shade. Then again, a substance, like a cow, will not be destroyed, if you paint it black – thus, it is not just perdurable, but also mutable.

Wolff's definition clearly is not meant as a strict division, but more as a hierarchy of substantiality – that is, we can speak of what is more accidental or substantial. Thus, we can change e.g. shape of a certain blob of colour, so that it will still remain a blob of this colour. Then again certain modifications of cow, such as tearing it apart, will undoubtedly destroy it. In addition, Wolff suggests we may define as proper substances those perdurables that will endure through any humanly conceivable change – these are essentially the simple substances. Then again, complex substances are in comparison accidental, because all their essential characteristics, such as figure and magnitude, are mere accidents. Thus, they can be only secondary substances.

Wolff ends his account of simple substances with a consideration of infinities. The characterisation of an infinite substance contains no surprises – infinite substance is incomparable with finite substances, but we can say that it has some analogical or eminent characteristics (eminence appears to be just a roundabout way to say that we really do not understand what it is). Then again, Wolff also makes some interesting remarks on mathematical infinities and infinitesimals. To put short, he admits that no mathematical infinities or infinitesimals actually exist, but also suggests that such fictions are useful in e.g. differential calculus.

So much for simple substances, now it is only relations we have to speak of.